关于画点连线的思考

type

status

date

slug

summary

前言

点和线是平面世界的基础，而画点连线更是基本操作。但是关于画点连线的方法，以及所能带来的思考，也是蛮有意思的。

在这片文章中，我会简单分析画点连线的基本方法。

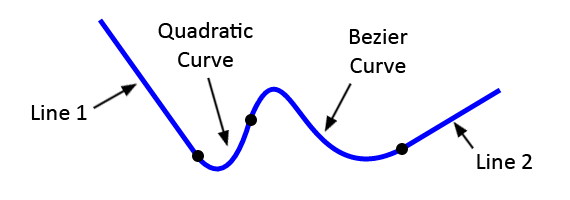
一起来画画

基本的画点连线

在这个章节，我们会创建 canvas 并且在上面获取鼠标的点的位置，并且将点放入一个数组存储，用直线连接起来。为了方便操作，我们使用 PIXI 这个库来简化操作。

具体的细节步骤如下：

首先使用 PIXI 初始化应用，创建一个舞台

然后获取 app.view，在 canvas 上面绑定点击事件

获取点击事件的具体的坐标，在对应位置绘制圆，将其放入数组存储

循环遍历数组，将两点依次连线，绘制出图形。

便可以得出以下的效果

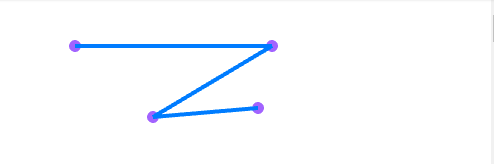
也可以在下面的环境中测试。

See the Pen xxgVzpW by kitety (@kitety) on CodePen.

上述的 demo 基本的实现了直线连接，但是表述很生硬，就是一段一段的线段，没有任何的美感。假如我们想要的是折线图，这就已经实现目标了，但是如果我们想要的是有点美感的曲线呢？这应该怎么做呢？这个时候就该我们的贝赛尔曲线登场了。

贝赛尔曲线

在维基百科中，他是这么解释的：在数学的数值分析领域中，贝塞尔曲线（英语：Bézier curve）是计算机图形学中相当重要的参数曲线。

感觉还是不理解，详细的过程可以参考这篇文章

本节不是对贝塞尔曲线做专业分析，如果有需要请参考其他网站，本文引用已经列举出来了。

二次贝赛尔曲线

大概的二次贝赛尔曲线就如下图所示：

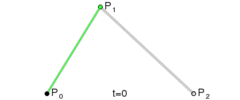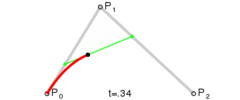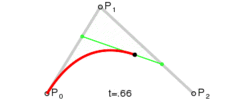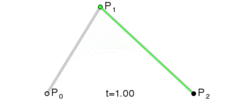
二次贝塞尔曲线由三个点P0、P1、P2来确定，这些点也叫做控制点。我们需要三个点就可以绘制出一条二次贝赛尔曲线，在canvas中的对应的方法就是quadraticCurveTo这个方法。

高次贝塞尔曲线

随着控制点的个数的增加，可以有三次，四次，N 次贝赛尔曲线，再多就不过多探讨。需要提示一下，绘制三次贝塞尔曲线的方法bezierCurveTo。

使用贝塞尔曲线绘制平滑曲线

要想绘制贝赛尔曲线，我们最简单的思路就是需要找准起点，控制点，终点。

最简单的就是假如我们有 A、B、C 三个点，我们需要绘制一条看似还算完美的曲线，我们应该怎么去思考呢？

我们会计算出 B 和 C 的中点 B1，以 A 为起点，B 为控制点，B1 为终点，最后将 B1、C 用直线链接。

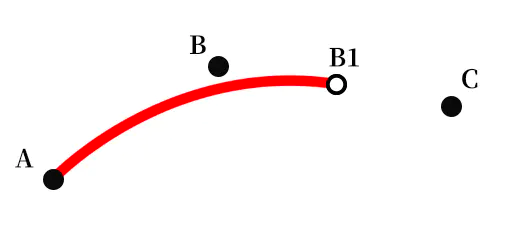
当然这只是三个点的情况，我们如此循环往复就可以绘制足够多的点了。

代码简析

这样我们就可以尽量绘制出比较平滑的曲线了

也可以在下面的环境中测试。

See the Pen eYgZjOM by kitety (@kitety) on CodePen.

上述的代码基本是实现了比较平滑的曲线，但是我们的还是会发现一些问题，就是在绘制的时候会出现画出来的线并没有经过所有点这种情况。而且参考的文章下面也有了类似的思考，一样抛出了这个问题。

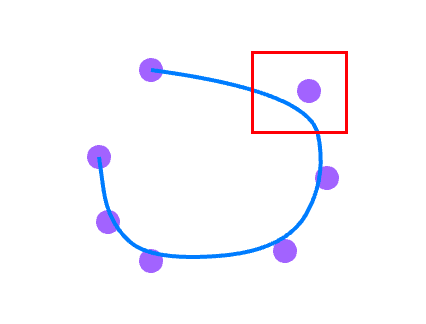
看来革命尚未成功，同志仍需努力啊。

相似三角形与贝赛尔曲线

其实在处理问题的时候，我们需要将问题简单化。比如在画点连线的过程中，我们很轻易的知道，两点之间肯定是连接直线就是最佳的。在需要曲线的时候，往往是两个点以上，因此我们就先画好三个点的曲线。

切线

如图，我们为三个点分了三种情况，其实前面两种很明显都是不合理的，都出现了没有必要的弯曲，只有最后一种稍显合理。

我们围绕三种情况 B 点的位置做出切线，发现只有看 k1 和 k2 的斜率几乎一直的时候才是比较合理的曲线，也就是三点中，曲线经过中间一点的切线和另外两点所成的直线平行的时候，这样的曲线才是比较合理的。

贝塞尔切线

而贝赛尔曲线的绘制图如下

我们截取中间的某个时刻会发现，很明显，贝塞尔曲线的起点和终点（其实也是控制点），他们的切线其实就是和轨迹相切的，这也是贝赛尔曲线的绘制方法，只不过起点和终点对应的就是t的0时刻和1时刻。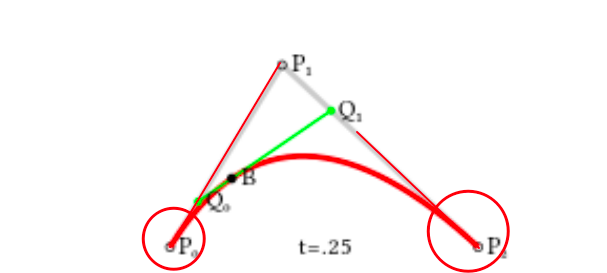

结论：我们绘制的曲线经过点的切线要和相邻的两点的直线平行，而贝赛尔曲线就是起点和终点平行，我们现在只需要找到其他的控制点绘制贝塞尔曲线即可。

解决问题

根据以上的思考，我们就有了后续的思路，我们分别需要在 AB 之间绘制一条贝赛尔曲线，B 为终点，切线相切；同时还要在 BC 之间绘制贝塞尔曲线，并且 B 点此时作为起点，要和上一条曲线经过 B 点的斜率一致。我们就有了上示的草稿图，并且可以得出一些相似的三角形。在当我们有了 A、B、C 三个点的坐标之后，还有对应的相似比 S1 和 S2，P1 和 P2 的坐标就是比较简单了。

接下来我们简单分析一下有 ABCDE 五个点的情况。我们五点中，中间的三个点是 BCD,我们都可以根据其各自的相邻两点做出对应的平行切线，并且每个点的切点上都可以找到对应两个点的控制点，根据控制点和各自的起点终点（其实也是控制点），我们可以绘制不同的红色举行的区域，分别可以用二次贝赛尔曲线绘制和三次贝赛尔曲线绘制。两点中有一个控制点的就是二次贝塞尔，比如 AB 之间；有两个控制点的就是三次贝塞尔，比如 BC 之间等。